F/T Sensors on-board IMU
The F/T sensors have an onboard IMU unit mounted on the STRAIN2 (the signal conditioning electronic board). The data from the IMU can be streamed out to the CAN bus with dedicated messages to complement the information from F/T sensor.
The IMU device is the BNO055 9-axis. The basic configuration of the IMU allows the user to directly read the raw data.
Measurement frame specifications
The F/T sensor reference frame and the IMU default reference frame are rigidly connected. The two frames are rotated with respect to each other.
The F/T reference frame can be determined by visual inspection (see Figure 1):
- the connection cable exits the sensor in the \(-x\) direction.
- the thin sensor cover (blue) indicates the \(+z\) direction.
- the \(y\) axis is determined according to a right-handed convention.
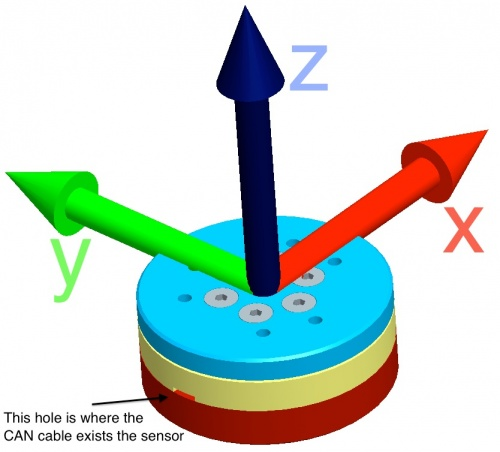
This reference frame is the one used to determine and transmit the forces and torques.
The IMU reference frame is defined w.r.t its location on the Strain2 PCB (see Figure 2). Its orientation can be also defined in terms of the F/T frame:
| IMU | F/T |
|---|---|
| \(x_{IMU}\) | \(-y_{FT}\) |
| \(y_{IMU}\) | \(-x_{FT}\) |
| \(z_{IMU}\) | \(-z_{FT}\) |
Finally, the IMU origin in the F/T frame coordinates are \(\left( 7.5, \; 8.6 \right)\) \(\text{mm}\).
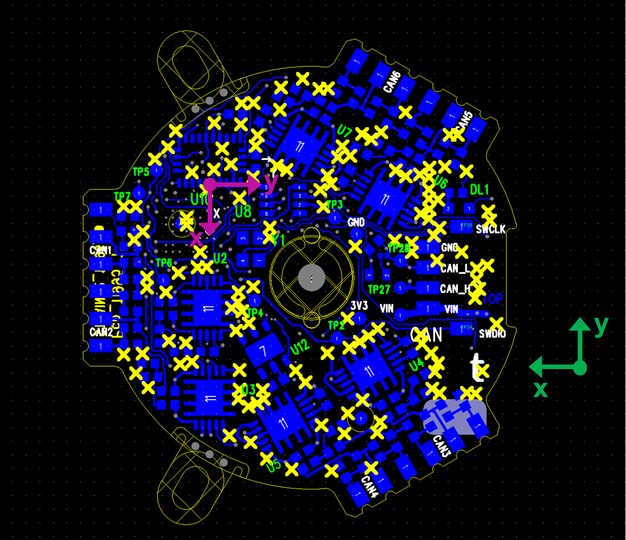
By configuring the firmware options, the two reference frames can be made coincident.
Nonetheless, to express accelerations in a different reference frame, one needs to account for non-inertial terms as explained in the following section.
Acceleration transformation with non-inertial terms
We have two reference frames rotated w.r.t. each other but rigidly connected, i.e. F/T and IMU reference frames. We measure accelerations with the IMU in its proper reference frame B, and we seek to transform the accelerations in the FT reference frame S.
Given the two relevant quantities:
- origin displacement of FT reference frame in IMU reference frame \({}^B o_S = (8.6, 7.5, 0)\) \(\text{mm}\);
- rotation matrix between the two reference frames \({}^SR_B\);
we can identify the transformation law as:
where the last two terms on the right are the non-inertial terms that appear in the reference frame transformation. The suffix A means that the quantity is calculated w.r.t. the inertial absolute reference frame.
For a more thorough and complete analysis, refer to this study 📚
Measurement of non-inertial terms in realistic scenarios
To assess the required level of precision in transforming the acceleration between the two dragged reference frames, we performed a few tests in a real world case, i.e. the iCub performing the Yoga Demo. In this demo the left foot is held on the ground and the robot balances over it moving the right leg. We logged both gyroscope and accelerometer data from all the F/T sensors and evaluated the non-inertial terms from the formula above.
As a test, we compared the transformed accelerations with and without the non-inertial components calculated according to equation above and the results are reported in the plotv below.
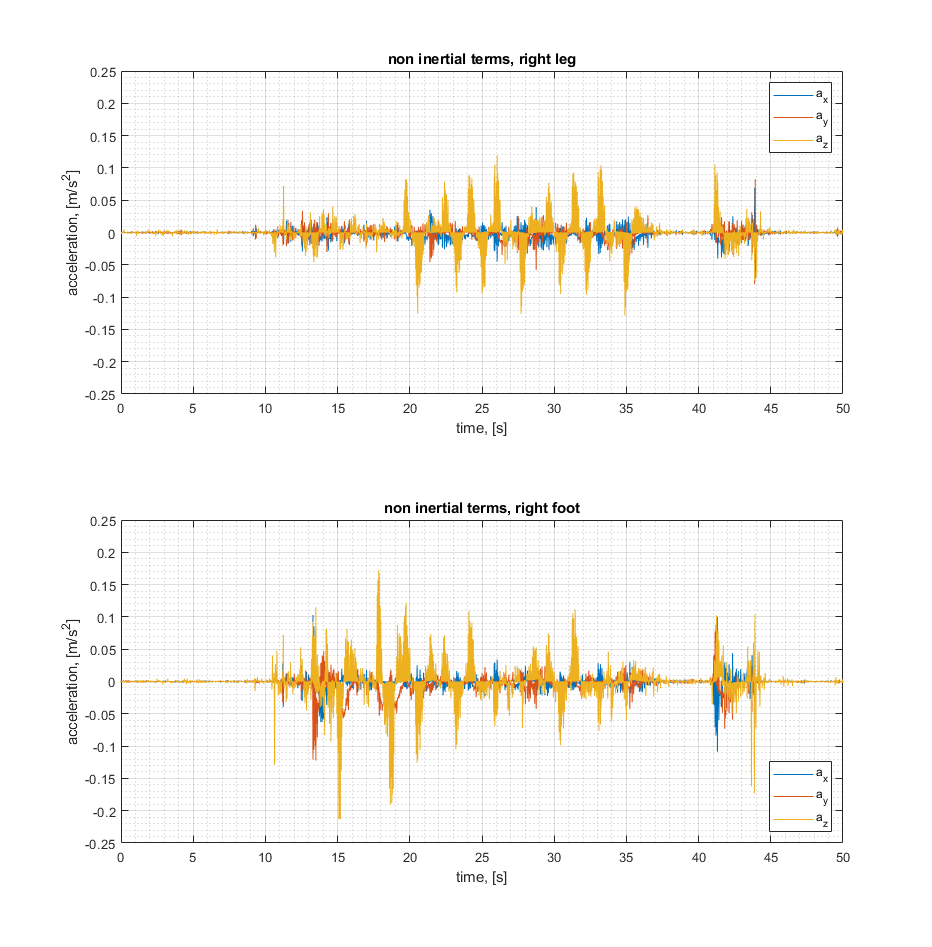
As a first approximation, in our use case we can neglect the effect of the drag non-inertial forces in the remapping of the accelerometer data. However, we choose an algorhithm approach to keep this possibility open in a next step.
To further pinpoint our assumption, we have evaluated the gravity vector as streamed from the BNO055 as \(g = 9.778\pm 0.021 m/s^2 \; (95\% \; \text{C.L.})\) which suffers also from systematic error of approx. \(0.4 m/s^2\), which is comparable to the error introduced by neglecting the non-inertial terms.
Outlook
As a future step, we may consider implementing the full transformation that includes the non-intertial terms.