Vergence, Version and Disparity
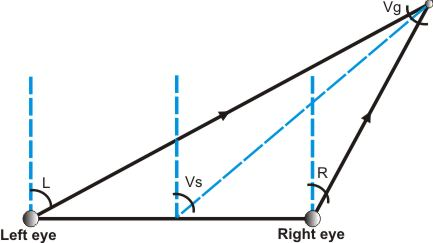
VERGENCE ANGLE
Vg = L - R
where L is the angle of the left camera with respect to the homed optical axis (which is the cameras z-axis) as in the figure above; R is the angle of the right camera with respect to the homed optical axis.
VERSION ANGLE
The version angle is the angle between the axis orthogonal to the baseline and passing through the baseline's midpoint and a line connecting this midpoint and the vergence point. The version angle satisfies the following nonlinear relation:
tan(Vs) = (tan(L) + tan(R)) / 2
However, the Firmware sends as version the following value:
Vs = (L + R) / 2
which holds for small angles (where tan(x)≈x), so that even though there is no lack of information since L and R angles can be accurately retrieved (see hereafter), the version Vs has physical meaning only for small values of Vs, L and R.
CONVERTING [VERGENCE|VERSION] TO [DECOUPLED L|R]
Combining the above equations yields:
L = Vs + Vg/2
R = Vs - Vg/2
DISPARITY
Disparity is defined as:
d = xl - xr
where xl is the left image normalized coordinate and xr is the right image normalized coordinate.
Object closer to the cameras than the current point of fixation, will elicit a positive disparity value.